Research Project C02

Combined multiphase flow, reactive transport processes, and mechanical deformation of the solid matrix in porous media are encountered in many important fields related to environmental applications. Typically, these processes occur and interact at different spatial and temporal scales. In C02, we consider multiple immiscible fluid and solid phases. At the pore scale, these phases are separated by interfaces, which move in the pore space due to processes like flow, precipitation and dissolution of crystals, or mechanical deformations driven by the fluid pressure or external stimulation. The main challenge is to understand the evolution of the interfaces at the pore scale, the impact on the pore geometry, and further on the REV-scale behaviour of the system. This makes traditional approaches that focus on single scale processes inadequate: at the smallest scales they are too complex and hence computationally prohibitive, while at the larger scale they ignore essential information provided by the smaller scales.

 The goal of the project  is to construct reliable and computationally affordable mathematical models for multi-scale problems in complex domains, which account for the interfaces evolving at the pore scale. Such issues will be addressed within a generic mathematical and computational framework.

We have developed multiple-diffuse interface models for fluid-solid interfaces. The first model describes the flow of one fluid phase and uses an Allen-Cahn evolution for the phase field variable. The second model describes the incompressible flow of two immiscible fluids and uses a ternary Cahn-Hilliard evolution for the phase-field variables. Both models modify the Navier-Stokes equations for incompressible fluid flow to hold only in the fluid volume fraction The solid phase is a mineral that can grow or shrink due to precipitation or dissolution, depending on the concentration of different solutes in the fluid phases. These concentrations are not known a-priori but represent model unknowns. The Cahn-Hilliard model has been shown to obey the second law of thermodynamics for a novel free-energy formulation.

For both models a sharp-interface formulation is recovered for vanishing interfacial width by using matched-asymptotic analysis. Notably, the Cahn-Hilliard model is able to realise Navier-slip conditions for solid-fluid interfaces in the limit.

Building on the pore-scale phase-field models, different REV-scale models have been derived. For the one-phase Allen-Cahn model this is achieved by assuming periodicity w.r.t. the fast variables at the micro-scale, and by employing homogenisation techniques. The result is a Darcy-type law at the REV scale, in which the porosity, the permeability and the effective diffusion still depend on the micro-scale characteristics (and in particular the amount of the mineral and its shape) encountered at each macro-scale point. These characteristics are described through cell problems in terms of the phase-field variable.

Further, for this REV-scale model, we have developed a multi-scale iterative scheme. In this scheme, the pore- and the REV-scale model components are coupled iteratively, which reduces significantly the complexity of the algorithm when compared to a monolithic approach. Next, linear iterative schemes building on the L-scheme are used to solve the non-linear cell problems at the pore scale. The macro-scale quantities like porosity, absolute permeability and the diffusion tensor are computed adaptively, based on an active-passive node strategy.

To derive a REV-scale model for the two-phase Cahn-Hilliard model, we considered it in the simplified geometry of a thin strip. The homogenised model, which is derived by transversal averaging, consists of up-scaled equations for ion transport and total flux, while the strongly non-linear phase-field equations do not up-scale. By using explicit upwinding for the transport terms in the numerical implementation, the cell problems still decouple and can be evaluated in parallel. We also find asymptotic consistency, that is, the sharp-interface limit of the up-scaled model is the same as the one obtained from up-scaling the sharp-interface limit.

For the Navier-Stokes Cahn-Hilliard model, we developed a finite-element method, with Taylor–Hood elements for the flow variables velocity and pressure, and second-order Lagrange elements for the ion concentration and the phase-field parameters. The implementation was done in DUNE-PDELab using ALU-Grid routines, thus being fully compatible with Dumux. Notably, this software framework allows for adaptive grid generation.

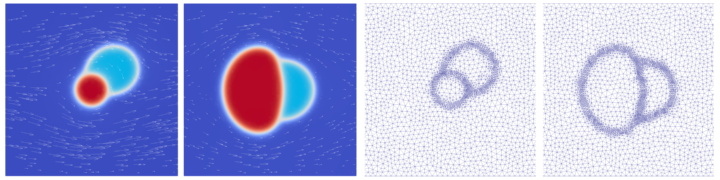
With this code, we ran a study in order to compare simulation results with experimental findings on enzymatically-induced calcite precipitation (EICP). This study investigates the growth of calcium-carbonate crystals in a micro-fluidic EICP experiment that consists of a setup of four pore bodies connected by pore throats. The model’s capability to reproduce the direction and volume of crystal growth has been analysed. The mechanisms that dominate crystal growth are complex. They depend on the local flow field as well as on concentrations of solutes. In particular, we succeeded to explain why crystal aggregates prefer to grow in up-stream flow direction and towards the center of the flow channels, where the volume growth rate is also higher due to better supply.

Starting from the ternary Cahn-Hilliard model we considered a simple, two-dimensional geometry of a thin strip, which can be seen as the representation of a single pore throat in a porous medium. In the limit case, when the ratio between the width and the length of the strip vanishes, we derived by transversal averaging an upscaled multi-scale model, which resembles classical lubrication limits: the phase-field equation has to be solved in cell problems at the pore scale to determine the position of interfaces. By investigating the sharp-interface limit of the multi-scale model, where the phase-field variable approaches zero, a closed REV-scale model was devised. The latter approach results in a new hyperbolic model, which can be understood as a generalisation of the classical Muskat-Leverett equations for two-phase flow towards our three-phasic setting.

To support the Pore Network Modelling with rigorous analysis, we presented  a reduced-dimensional asymptotic modelling approach for the analysis of two-phase flow in a thin cylinder. It accounts for flows seep through as well as chemical reactions on the lateral surface of the cylinder. We have rigorously derived effective equations in one-space dimension that are sensitive to the actual capillary number and a Damköhler-like number for chemical reaction kinetics at the lateral boundary. This model can contribute to enable efficient time-resolved simulations in the pore throats.

We made contributions to the Salt Vision topic. During FP 2, Pore Network Modelling turned out to be an important tool to understand the migration of salt to the surface of a porous material, see A02. In cooperation with A02 and A05 we developed and analysed in various Pore Network Models for single-phase flow with salt precipitation at the pore walls. Because the precipitation leads to pore-space alterations, a key issue in modelling such effects is how this affects the throat transmissibility. Different concepts have been considered for determining the amount of precipitate in the throats. We contributed with a phase-field model for chemically reacting one-phase flow inside the pore throat.

To govern evaporation-driven salt precipitation, we extended in cooperation with CX3 the Pore Network Model approach to account for two-phase, multi-component flow and heat conduction. Similar as in a REV-scale model, the change in the pore space and also pore-scale heterogeneities are considered. In DuMux-based numerical experiments, it has been shown that the presented model is able to investigate accurately the influence of pore-space alterations, the brine-air interface location and local heterogeneities on flow, salt transport, precipitation and evaporation.

Based on these achievements, we will  explore additional physical processes that are directly linked to the Salt Vision, involving either subflorescence or efflorescence salts. In particular, this will include studies of effects driven by mechanical deformation, gas dissolution, evaporation and convection-dominated flow, all of which are being studied experimentally in SFB 1313. A specific focus will be on integrating efficient numerical tools for two-scale models, which utilise data-integrated simulation methods and coupling techniques from Project Area D. We will continue to validate our mathematical models through analytical investigations, and will contribute to REV-scale and Pore Network Modelling in Project Area A with homogenised and dimensionally-reduced models. We plan to advance our research on the Muskat-Leverett model in thin graph-like networks, with a particular focus on bifurcated geometries. Deriving one-dimensional models with accurate coupling conditions at vertices will enhance predictions of multiphase flow in fracture systems.

We work in close cooperation with the Computational Mathematics group (CMAT) at Hasselt University. The upscaling of phase field models was done in collaboration with Hasselt University, sharing knowledge of homogenisation techniques for different regimes and geometric assumptions. In particular for the upscaling in a thin strip our cooperation includes surface tension effects between two fluid phases. The development of a multi-scale iterative scheme for the upscaled Allen-Cahn model is also a collaboration with Hasselt University.

We cooperate on the topic of upscaled models for incompressible two-phase flow, including hysteresis.