Research Project B03

Heterogeneous multi-scale methods for two-phase flow in dynamically fracturing porous media

true" ? copyright : '' }

People

Maximilian Hörl

Taras Mel'nyk (associated research project I-08)

Samuel Burbulla (Alumnus)

Jim Magiera (Alumnus)

David Seus (Alumnus)

Publications

  1. Conference papers

    1. Gander, M. J., Lunowa, S. B., & Rohde, C. (2022). Consistent and Asymptotic-Preserving Finite-Volume Robin Transmission Conditions for Singularly Perturbed Elliptic Equations. In S. C. Brenner, E. Chung, A. Klawonn, F. Kwok, J. Xu, & J. Zou (Eds.), Domain Decomposition Methods in Science and Engineering XXVI (pp. 443–450). Springer International Publishing. https://doi.org/10.1007/978-3-030-95025-5_47
    2. Burbulla, S., & Rohde, C. (2020). A Fully Conforming Finite Volume Approach to Two-Phase Flow in Fractured Porous Media. In R. Klöfkorn, E. Keilegavlen, F. A. Radu, & J. Fuhrmann (Eds.), Finite Volumes for Complex Applications IX - Methods, Theoretical Aspects, Examples (pp. 547–555). Springer International Publishing. https://doi.org/10.1007/978-3-030-43651-3

  2. Monographs

    1. Burbulla, S. (2023). Mixed-dimensional modeling of flow in porous media. Dissertation thesis, University of Stuttgart. https://doi.org/10.18419/opus-12712

  3. (Journal-) Articles

    1. Hörl, M., & Rohde, C. (2024). Rigorous derivation of discrete fracture models for Darcy flow in the limit of vanishing aperture. Networks and Heterogeneous Media, 19, 114–156. https://doi.org/10.3934/nhm.2024006
    2. Mel’nyk, T., & Rohde, C. (2024). Puiseux asymptotic expansions for convection-dominated transport problems in thin graph-like networks: Strong boundary interactions. Asymptotic Analysis, 137, 27–52. https://doi.org/10.3233/asy-231876
    3. Mel’nyk, T., & Durante, T. (2024). Spectral problems with perturbed Steklov conditions in thick junctions with branched structure. Applicable Analysis, 103, Article 15. https://doi.org/10.1080/00036811.2024.2322644
    4. Mel’nyk, T., & Rohde, C. (2024). Reduced-dimensional modelling for nonlinear convection-dominated flow in cylindric domains. Nonlinear Differential Equations and Applications NoDEA, 31, Article 6. https://doi.org/10.1007/s00030-024-00997-6
    5. Mel’nyk, T., & Rohde, C. (2024). Asymptotic expansion for convection-dominated transport in a thin graph-like junction. Analysis and Applications, 22, 833–879. https://doi.org/10.1142/s0219530524500040
    6. Mel’nyk, T., & Rohde, C. (2024). Asymptotic approximations for semilinear parabolic convection-dominated transport problems in thin graph-like networks. Journal of Mathematical Analysis and Applications, 529. https://doi.org/10.1016/j.jmaa.2023.127587
    7. Burbulla, S., Formaggia, L., Rohde, C., & Scotti, A. (2023). Modeling fracture propagation in poro-elastic media combining phase-field and discrete fracture models. Computer Methods in Applied Mechanics and Engineering, 403. https://doi.org/10.1016/j.cma.2022.115699
    8. Burbulla, S., Hörl, M., & Rohde, C. (2023). Flow in Porous Media with Fractures of Varying Aperture. SIAM Journal on Scientific Computing, 45, A1519–A1544. https://doi.org/10.1137/22M1510406
    9. Gander, M. J., Lunowa, S. B., & Rohde, C. (2023). Non-Overlapping Schwarz Waveform-Relaxation for Nonlinear Advection-Diffusion Equations. SIAM Journal on Scientific Computing, 45, A49–A73. https://doi.org/10.1137/21m1415005
    10. Seus, D., Radu, F. A., & Rohde, C. (2023). Towards hybrid two-phase modelling using linear domain decomposition. Numerical Methods for Partial Differential Equations, 39, 622–656. https://doi.org/10.1002/num.22906
    11. Burbulla, S., Dedner, A., Hörl, M., & Rohde, C. (2022). Dune-MMesh: The Dune Grid Module for Moving Interfaces. Journal of Open Source Software, 7. https://doi.org/10.21105/joss.03959
    12. Burbulla, S., & Rohde, C. (2022). A finite-volume moving-mesh method for two-phase flow in fracturing porous media. Journal of Computational Physics. https://doi.org/10.1016/j.jcp.2022.111031
    13. Berre, I., Boon, W. M., Flemisch, B., Fumagalli, A., Gläser, D., Keilegavlen, E., Scotti, A., Stefansson, I., Tatomir, A., Brenner, K., Burbulla, S., Devloo, P., Duran, O., Favino, M., Hennicker, J., Lee, I.-H., Lipnikov, K., Masson, R., Mosthaf, K., et al. (2021). Verification benchmarks for single-phase flow in three-dimensional fractured porous media. Advances in Water Resources, 147. https://doi.org/10.1016/j.advwatres.2020.103759
    14. Koch, T., Gläser, D., Weishaupt, K., Ackermann, S., Beck, M., Becker, B., Burbulla, S., Class, H., Coltman, E., Emmert, S., Fetzer, T., Grüninger, C., Heck, K., Hommel, J., Kurz, T., Lipp, M., Mohammadi, F., Scherrer, S., Schneider, M., et al. (2021). DuMux 3 - an open-source simulator for solving flow and transport problems in porous media with a focus on model coupling. Computers & Mathematics with Applications, 81, 423–443. https://doi.org/10.1016/j.camwa.2020.02.012
    15. Köppel, M., Martin, V., Jaffré, J., & Roberts, J. E. (2019). A Lagrange multiplier method for a discrete fracture model for flow in porous media. Computational Geosciences, 23, 239–253. https://doi.org/10.1007/s10596-018-9779-8
    16. Seus, D., Mitra, K., Pop, I. S., Radu, F. A., & Rohde, C. (2018). A linear domain decomposition method for partially saturated flow in porous media. Computer Methods in Applied Mechanics and Engineering, 333, 331–355. https://doi.org/10.1016/j.cma.2018.01.029

Published data sets

  1. Gläser, D., Seeland, A., Schulze, K., & Burbulla, S. (2023). Verification benchmarks for single-phase flow in three-dimensional fractured porous media: DuMuX source code [DaRUS]. https://doi.org/10.18419/DARUS-3228
  2. Burbulla, S., Hörl, M., & Rohde, C. (2022). Replication Data for: Flow in Porous Media with Fractures of Varying Aperture [DaRUS]. https://doi.org/10.18419/DARUS-3227
  3. Burbulla, S., Hörl, M., & Rohde, C. (2022). Source Code for: Flow in Porous Media with Fractures of Varying Aperture [DaRUS]. https://doi.org/10.18419/DARUS-3012

Research

About this Project

Project B03 investigates the evolution of fracture networks in fluid-filled poroelastic media, focusing on the interplay between fluid flow and solid deformation. We model incompressible single- and two-phase flow in fractured media on a continuum-mechanical REV scale and employ a discrete fracture approach, treating fractures as dynamic codimension-one manifolds with their own flow equations. Our goal is to develop models and numerical methods for increasing geometric and flow complexity, particularly when fracture propagation is driven by fluid pressure and stress. In such cases, the fracture network becomes an evolving, multi-scale free boundary problem.

 

 

Pressure field for single-phase flow in a fractured three-dimensional porous medium.
Image: Samuel Burbulla
Numerical results for the multi-scale method. The pressure field of the discrete fracture model (left) is coupled to a phase-field model (right) that governs the fracture tip movement in a small region around it. The grey shadow indicates bulk porous medium with higher Griffith critical energy.
Image: Samuel Burbulla

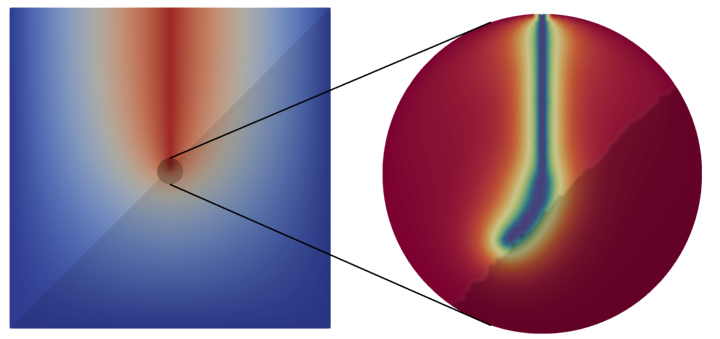
Results

Funding Period 1

During the first funding period, we have developed numerical models and discretisation methods for simulating evolving fracture networks involving two-phase flow in both fractures and the surrounding porous medium. A key innovation is a finite-volume method capable of handling fracture propagation on a conforming mesh. For a geometrically prescribed fracture evolution, an existing moving-mesh concept has been further developed to provide a mesh displaying the discrete fracture as connected mesh facets at any discrete time-step.  All code has been implemented within the DUNE framework and integrated into DuMuX to simulate two-phase flow scenarios with prescribed fracture propagation, bifurcation, and intersection.

In addition, we developed a heterogeneous multi-scale method for single-phase flow, enabling the tracking of fracture propagation using a phase-field approach as the microscopic model. The phase-field equation is solved locally in a small region near the fracture tip to capture the fine-scale dynamics of the fracture evolution.

Funding Period 2

In the current (second) funding period, we have developed discrete fracture models for single-phase flow in porous media with spatially varying fracture apertures, derived via formal vertical averaging. These models generalize a widely used constant-aperture model and were validated against three-dimensional discontinuous Galerkin simulations. We also pursued a rigorous analysis of the vanishing-aperture limit, for the first time considering curved fractures with variable aperture. Accounting for different hydraulic conductivities in the bulk and fractures, we identified various discrete fracture models exhibiting conduit- or barrier-type coupling. In collaboration with projects B04, D03, and INF, we are developing a Bayesian framework to quantify the validity range of these models.

Illustration of the limit of vanishing aperture for a curved fracture with spatially varying aperture.
Image: Maximilian Hörl

We also advanced flow modelling in fracturing poroelastic media, coupling fracture propagation and opening with hydromechanical forces. Building on our earlier work, we introduced a thermodynamically consistent model and a corresponding discontinuous Galerkin moving-mesh discretisation. The model explicitly resolves the fracture geometry and uses a local phase-field method for propagation, maintaining geometric flexibility. Additionally, we developed robust domain decomposition methods for two-phase flow in fractured media, ensuring efficiency and convergence across varying models and capillary regimes.

Horizontal displacement for fluid-driven fracture propagation. Two fractures join and create a connected fracture network. From the tips of the vertical part propagation continues in a diagonal direction.
Image: Samuel Burbulla

To support the Salt Vision and pore network modelling in project A02, we studied the dimensional reduction of evolution equations in three-dimensional cylindrical networks to one-dimensional graphs. Our novel asymptotic approach, based on rigorous multi-scale expansions, addresses convection-dominated transport problems in linear, semilinear, and quasilinear settings while accounting for boundary interactions with different intensities and geometric variations.

Future Work

We aim to advance the rigorous validation of discrete fracture models for nonlinear two-phase flow—both partially and fully saturated—accounting for planar and curved fractures with varying apertures. Building on our analytical investigations, we will extend our heterogeneous multi-scale method to track the evolution of fracture networks in three-dimensional porous media under complex two-phase flow conditions. In collaboration with project B01, we will more accurately describe the local propagation of crack tips. As a contribution to the Salt Vision, we will work with project C02 to incorporate precipitation and dissolution effects, enabling the simulation of temporal changes in fracture aperture. The newly developed discrete fracture models will undergo quantitative validation, including comparisons with experimental data in collaboration with projects B05 and Z02.

In the final project phase, we will investigate elastic wave dynamics, focusing on the propagation of acoustic waves in fractured poroelastic media in saturated two-phase flow. These tools will further support the Salt Vision through the study of carbonation processes and subflorescence salt formation in fractured soil systems. The project will conclude with a study on the acoustic response of fully saturated two-phase flow in fractured porous media.

International Cooperation

University of Bergen, Norway

We collaborate with Mercator and Humboldt fellow Prof. Kundan Kumar on the rigorous derivation of discrete fracture models in poroelastic media in the limit of vanishing fracture aperture. Together with Mercator Fellow Prof. Florin Radu, we are developing robust domain decomposition methods for simulating two-phase flow in fractured porous media.

Politecnico di Milano, Italy

In collaboration with Prof. Luca Formaggia and Prof. Anna Scotti, we are advancing a heterogeneous multi-scale method for modelling two-phase flow in poroelastic media. This approach tracks the temporal evolution of fracture networks through a combined discrete fracture and phase-field approach.

For further information please contact

This image shows Christian Rohde

Christian Rohde

Prof. Dr. rer. nat.

Deputy Spokesperson, Project Leader, Research Projects A02, B03, C02, Project MGK

To the top of the page