People
David Seus (Alumnus)
Research
About this Project
Project B03 investigates the evolution of fracture networks in fluid-filled poroelastic media, focusing on the interplay between fluid flow and solid deformation. We model incompressible single- and two-phase flow in fractured media on a continuum-mechanical REV scale and employ a discrete fracture approach, treating fractures as dynamic codimension-one manifolds with their own flow equations. Our goal is to develop models and numerical methods for increasing geometric and flow complexity, particularly when fracture propagation is driven by fluid pressure and stress. In such cases, the fracture network becomes an evolving, multi-scale free boundary problem.
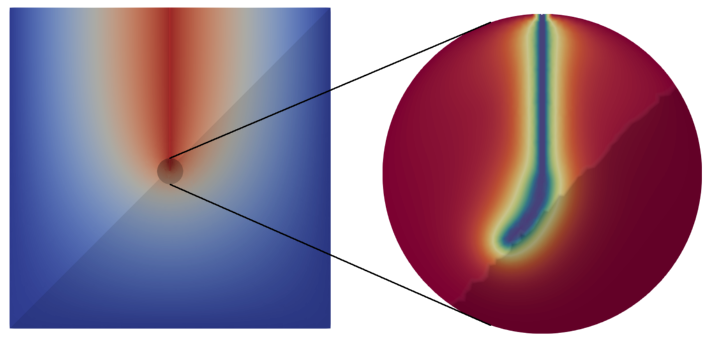
Results
Funding Period 1
During the first funding period, we have developed numerical models and discretisation methods for simulating evolving fracture networks involving two-phase flow in both fractures and the surrounding porous medium. A key innovation is a finite-volume method capable of handling fracture propagation on a conforming mesh. For a geometrically prescribed fracture evolution, an existing moving-mesh concept has been further developed to provide a mesh displaying the discrete fracture as connected mesh facets at any discrete time-step. All code has been implemented within the DUNE framework and integrated into DuMuX to simulate two-phase flow scenarios with prescribed fracture propagation, bifurcation, and intersection.
In addition, we developed a heterogeneous multi-scale method for single-phase flow, enabling the tracking of fracture propagation using a phase-field approach as the microscopic model. The phase-field equation is solved locally in a small region near the fracture tip to capture the fine-scale dynamics of the fracture evolution.
Funding Period 2
In the current (second) funding period, we have developed discrete fracture models for single-phase flow in porous media with spatially varying fracture apertures, derived via formal vertical averaging. These models generalize a widely used constant-aperture model and were validated against three-dimensional discontinuous Galerkin simulations. We also pursued a rigorous analysis of the vanishing-aperture limit, for the first time considering curved fractures with variable aperture. Accounting for different hydraulic conductivities in the bulk and fractures, we identified various discrete fracture models exhibiting conduit- or barrier-type coupling. In collaboration with projects B04, D03, and INF, we are developing a Bayesian framework to quantify the validity range of these models.
We also advanced flow modelling in fracturing poroelastic media, coupling fracture propagation and opening with hydromechanical forces. Building on our earlier work, we introduced a thermodynamically consistent model and a corresponding discontinuous Galerkin moving-mesh discretisation. The model explicitly resolves the fracture geometry and uses a local phase-field method for propagation, maintaining geometric flexibility. Additionally, we developed robust domain decomposition methods for two-phase flow in fractured media, ensuring efficiency and convergence across varying models and capillary regimes.
To support the Salt Vision and pore network modelling in project A02, we studied the dimensional reduction of evolution equations in three-dimensional cylindrical networks to one-dimensional graphs. Our novel asymptotic approach, based on rigorous multi-scale expansions, addresses convection-dominated transport problems in linear, semilinear, and quasilinear settings while accounting for boundary interactions with different intensities and geometric variations.
Future Work
We aim to advance the rigorous validation of discrete fracture models for nonlinear two-phase flow—both partially and fully saturated—accounting for planar and curved fractures with varying apertures. Building on our analytical investigations, we will extend our heterogeneous multi-scale method to track the evolution of fracture networks in three-dimensional porous media under complex two-phase flow conditions. In collaboration with project B01, we will more accurately describe the local propagation of crack tips. As a contribution to the Salt Vision, we will work with project C02 to incorporate precipitation and dissolution effects, enabling the simulation of temporal changes in fracture aperture. The newly developed discrete fracture models will undergo quantitative validation, including comparisons with experimental data in collaboration with projects B05 and Z02.
In the final project phase, we will investigate elastic wave dynamics, focusing on the propagation of acoustic waves in fractured poroelastic media in saturated two-phase flow. These tools will further support the Salt Vision through the study of carbonation processes and subflorescence salt formation in fractured soil systems. The project will conclude with a study on the acoustic response of fully saturated two-phase flow in fractured porous media.
International Cooperation
University of Bergen, Norway
We collaborate with Mercator and Humboldt fellow Prof. Kundan Kumar on the rigorous derivation of discrete fracture models in poroelastic media in the limit of vanishing fracture aperture. Together with Mercator Fellow Prof. Florin Radu, we are developing robust domain decomposition methods for simulating two-phase flow in fractured porous media.
Politecnico di Milano, Italy
In collaboration with Prof. Luca Formaggia and Prof. Anna Scotti, we are advancing a heterogeneous multi-scale method for modelling two-phase flow in poroelastic media. This approach tracks the temporal evolution of fracture networks through a combined discrete fracture and phase-field approach.
For further information please contact

Christian Rohde
Prof. Dr. rer. nat.Deputy Spokesperson, Project Leader, Research Projects A02, B03, C02, Project MGK





