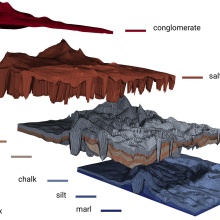
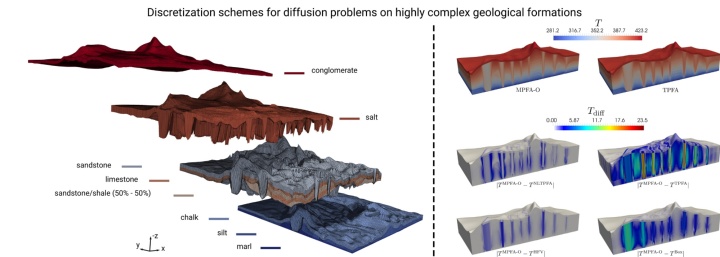
Our next SFB 1313 publication, entitled „Comparison of finite-volume schemes for diffusion problems”, was published by Martin Schneider, Dennis Gläser, Bernd Flemisch, and Rainer Helmig.
Abstract
We present an abstract discretization framework and demonstrate that various cell-centered and hybrid finite-volume schemes fit into it. The different schemes considered in this work are then analyzed numerically for an elliptic model problem with respect to the properties consistency, coercivity, extremum principles, and sparsity. The test cases presented comprise of two- and three dimensional setups, mildly and highly anisotropic tensors and grids of different complexities. The results show that all schemes show a similar convergence behavior, except for the two-point flux approximation scheme, and seem to be coercive. Furthermore, they confirm that linear schemes, in contrast to nonlinear schemes, are in general neither positivity-preserving nor satisfy discrete minimum or maximum principles